[Flare On 12] Writeup
Flare On 12
This is my first year playing Flare On challenge after nearly one year of learning Reverse Engineering, and luckily despite company’s tasks and schoolwork, I’ve managed become one of many Flare On finishers. Here’s my write up for my favourite Flare challenges this year.
2-Project Chimera
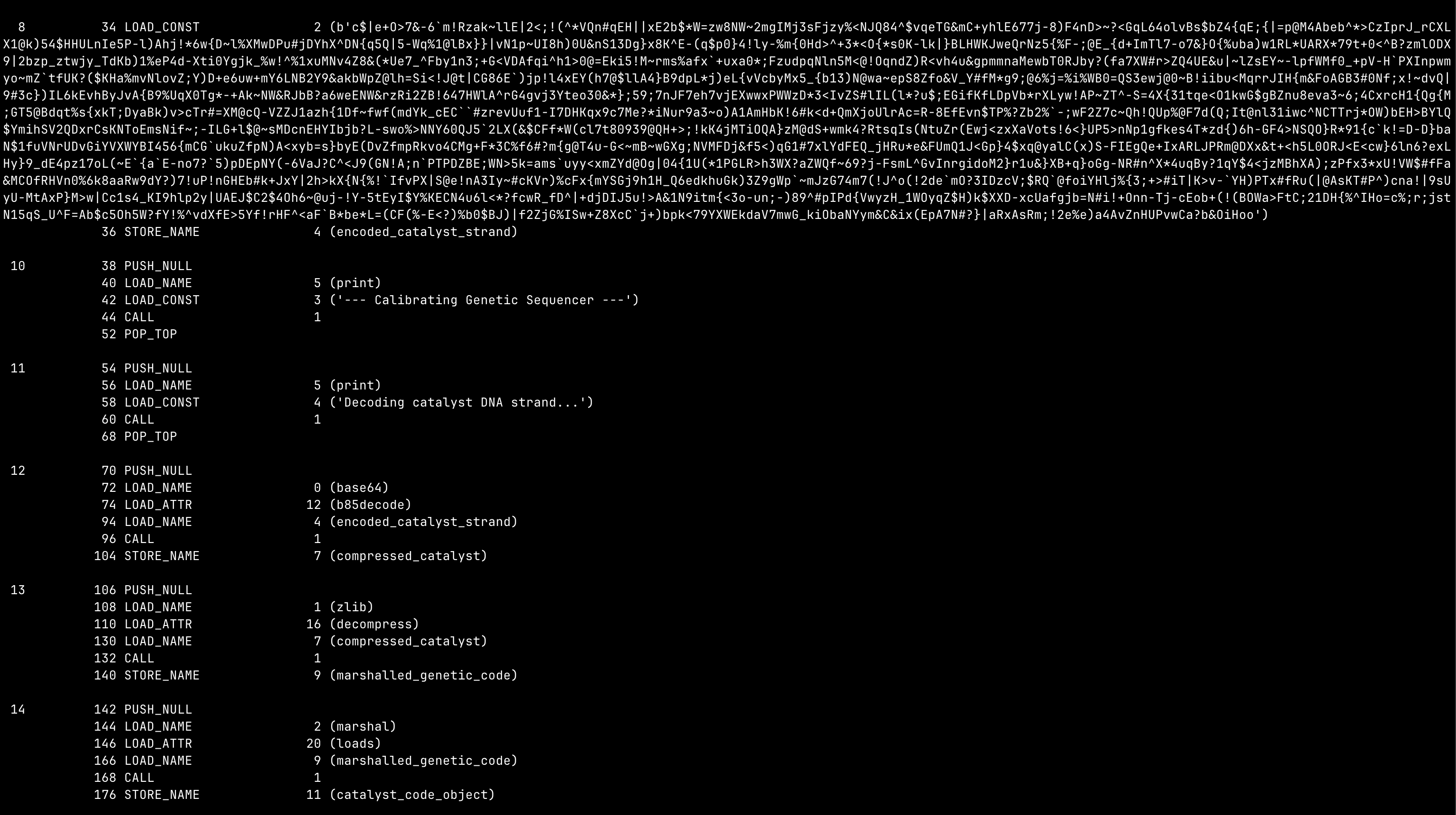
This challenge provides a python file that decompressed and execute python bytecode via marshal.loads() and then exec()
I used dis.dis() on various python version and figure out the version was python3.12 (I think this is the hardest part of the challenge, lmao):
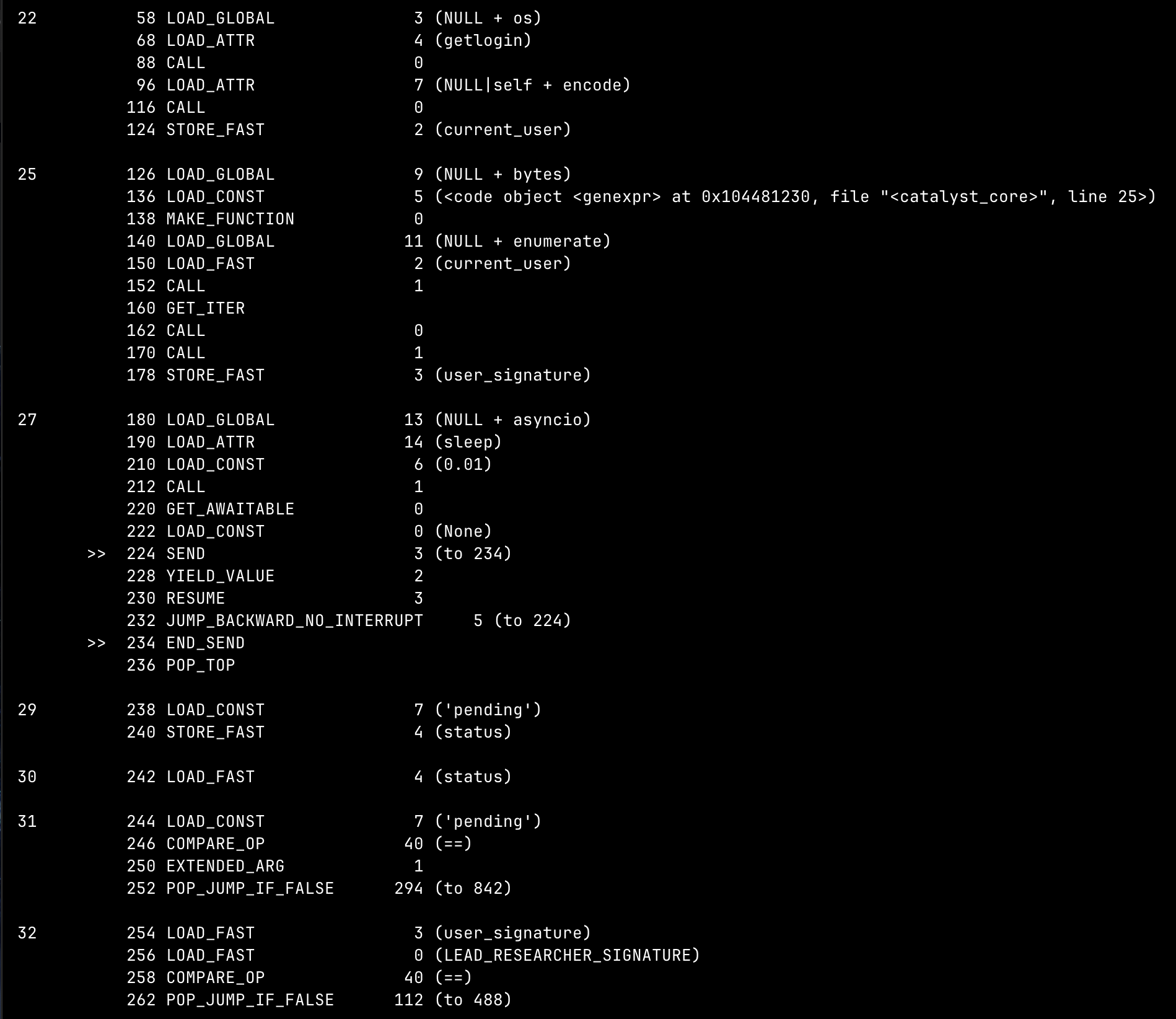
The dissassembled python bytecode shows that the program loaded a base85-decoded bytes, and the decompress it into another block of python bytecode, disassemble the bytes again and now we have the actual code that performs authorization. It’s simply just take your PC username (via os.getlogin()) transformed it and check if it matches the target string:
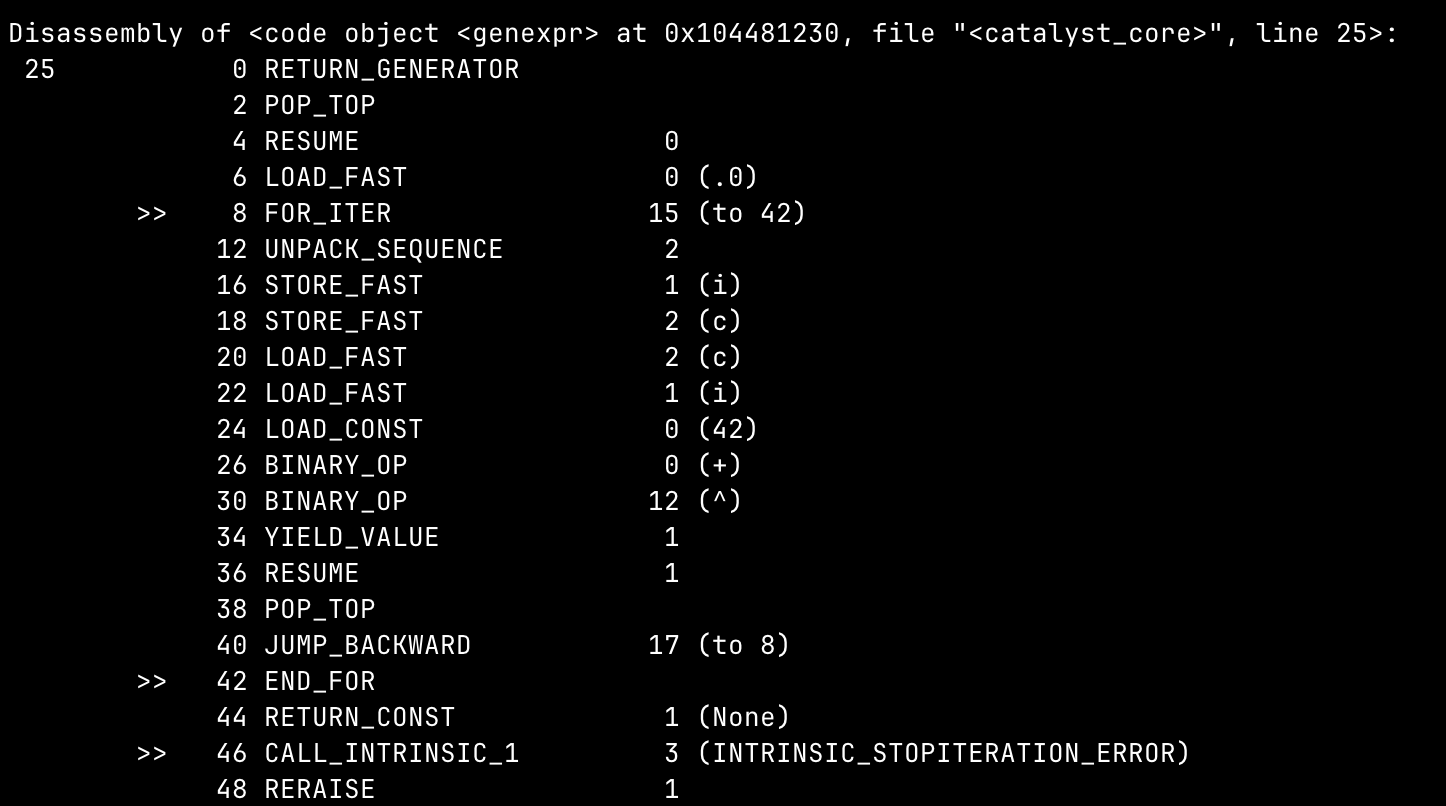
It calls object <genexpr> to transform the PC username
which is just simply
1
user_signature = bytes([username[i] ^ (i + 42) for i in range(len(username))])
Then check if the user_signature matches with the LEAD_RESEARCHER_SIGNATURE, if matches, it use that username as the key to perform RC4 decryption on the flag. I solved this with this script:
1
2
3
4
5
6
7
8
9
10
from Crypto.Cipher import ARC4
ct = b'r2b-\r\x9e\xf2\x1fp\x185\x82\xcf\xfc\x90\x14\xf1O\xad#]\xf3\xe2\xc0L\xd0\xc1e\x0c\xea\xec\xae\x11b\xa7\x8c\xaa!\xa1\x9d\xc2\x90'
LEAD_RESEARCHER_SIGNATURE = b"m\x1b@I\x1dAoe@\x07ZF[BL\rN\n\x0cS"
key = bytes([LEAD_RESEARCHER_SIGNATURE[i] ^ (i + 42) for i in range(len(LEAD_RESEARCHER_SIGNATURE))])
cipher = ARC4.new(key=key)
flag = cipher.decrypt(ct)
print(flag)
Flag: Th3_Alch3m1sts_S3cr3t_F0rmul4@flare-on.com
5 - ntfsm
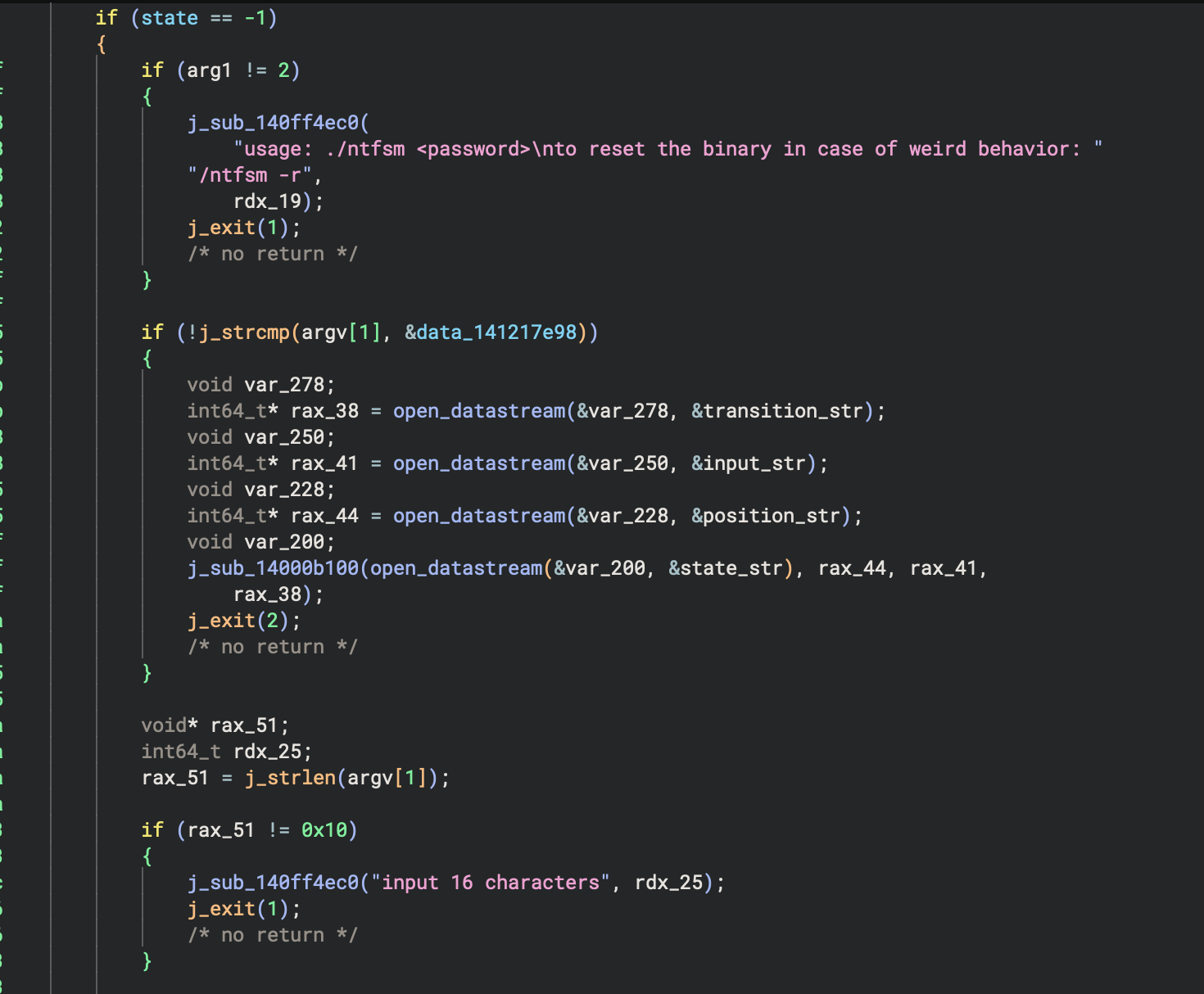
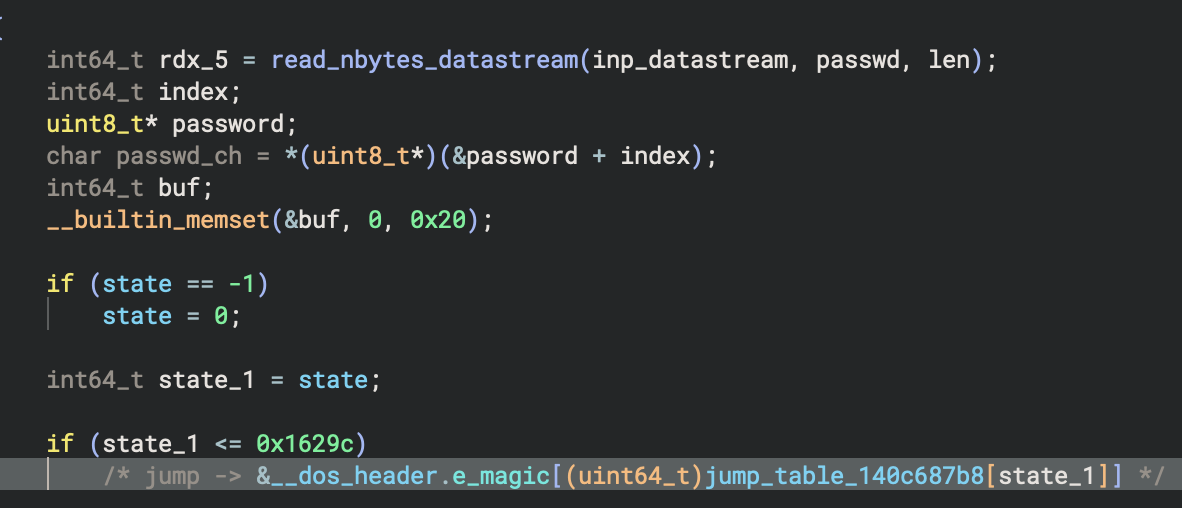
For this challenge, my first impression is that it took too long to load into IDA so I used Binary Ninja instead. It took Binja 3-4 hours to perform thorough analysis on the binary. Initially, the program requires user to input a 16-byte long argument string as the password
Then it perform password processing, in what seems to be a very big switch case statement:
Having the jumptable of the switch case statement. Knowing the address of the jumptable and the mechanism to compute the case address, I wrote this small script for ease of finding the address of each case in the statement:
1
2
3
4
5
6
7
8
9
header = 0x140000000
start_table = 0xc67bb8
end_table = start_table + 0x1629d * 4
jump_table = list(open('ntfsm.exe', 'rb').read()[start_table:end_table])
jump_table = [int.from_bytes(jump_table[i:i+4], 'little') for i in range(0, len(jump_table), 4)]
print(hex(header + jump_table[0])) #Change index to find the wanted case
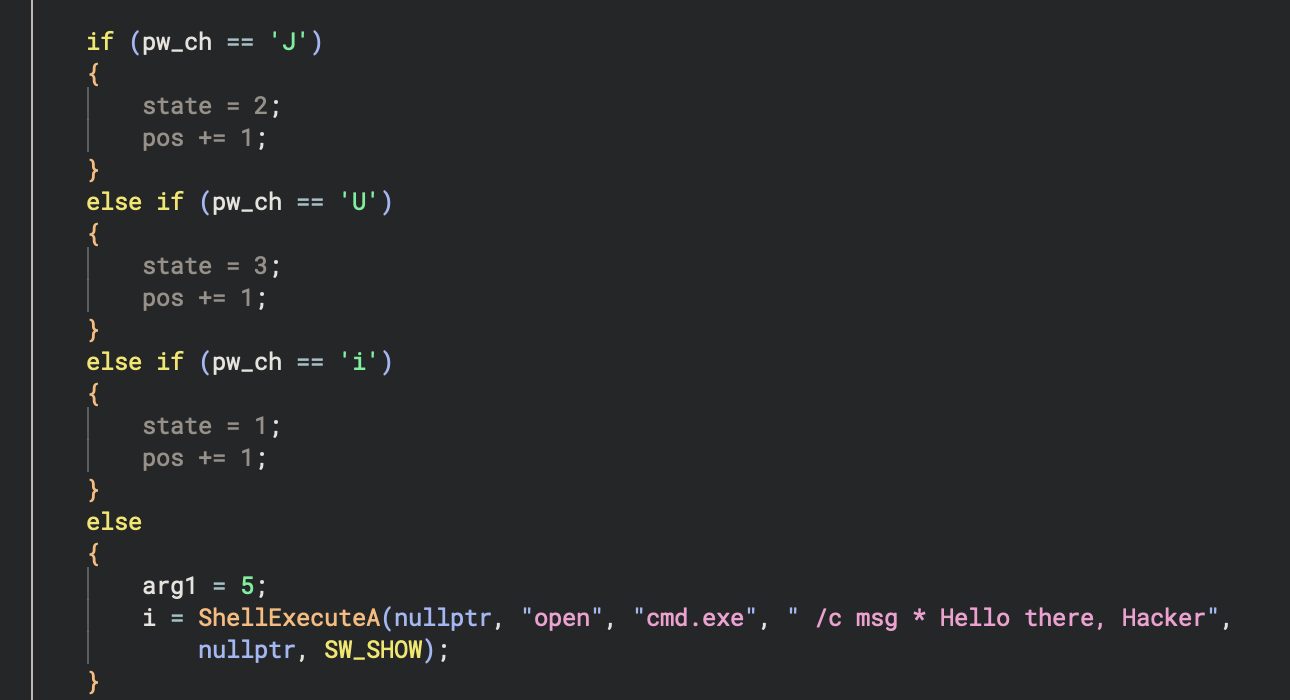
Statically analyze some of the branch over 90000 ones, we can easily see the pattern that, for each state there’s a different transition (next state) based on the current byte of the input, if the current byte of the input doesn’t match any case it doesn’t increase the pos, and it perform some action like spamming open "cmd.exe" or open rick-roll videos :v.
Then the index is increased and it returns to the main flow by resetting the value of rsp so that when retn (pop rip) is called, the instruction pointer returns to the main.
140c687ae 4881c490930500 add rsp, 0x59390
140c687b5 5f pop rdi
140c687b6 c3 retn
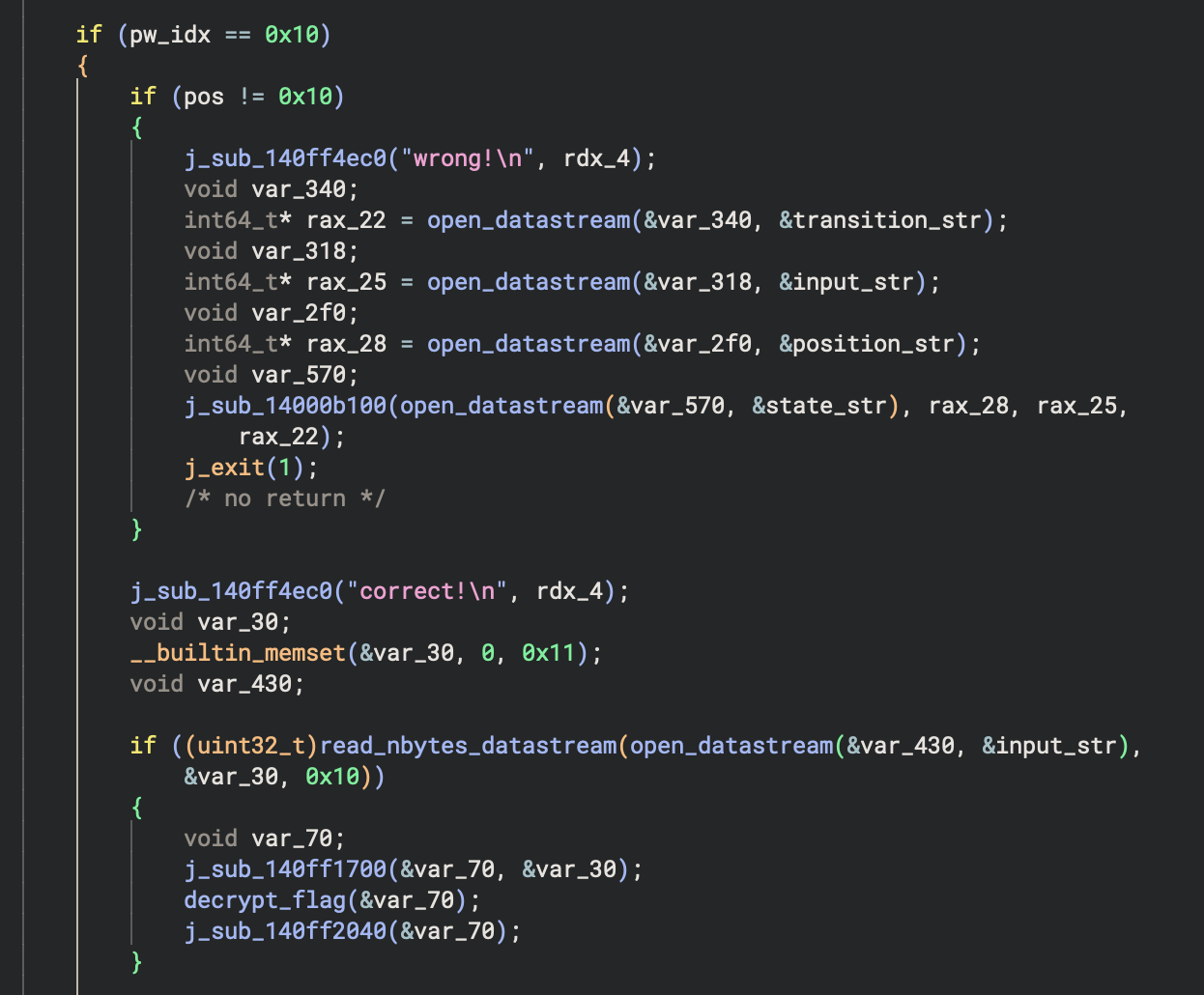
There it checks if the program has been over 15 transitions (16 states or not). If yes, it checks if the input successfully stays in transition range of all state it has been through (pos == 16), then it decrypts and give users the flag:
Bringing in everything together, the binary is just a sparse graph with states as vertices and transitions as edges. Analyzing further, we can see that there’s some state that perform no transitions no matter what the input is, such as:
These are the fail states. Now everything, is clear this is called a Finite State Machine in automata, and our job is to find the final success state through our input. What we need to do now is the extract the states, the transitions, and filter out the fail states. Analyzing the disassembly pattern, for the intermediate states:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
140860281 0fb6442430 movzx eax, byte [rsp+0x30 {pw_ch}]
140860286 8884248cbb0300 mov byte [rsp+0x3bb8c {arg_3bb8c}], al
14086028d 80bc248cbb03004a cmp byte [rsp+0x3bb8c {arg_3bb8c}], 'J'
140860295 7437 je 0x1408602ce
140860297 80bc248cbb030055 cmp byte [rsp+0x3bb8c {arg_3bb8c}], 'U'
14086029f 744e je 0x1408602ef
1408602a1 80bc248cbb030069 cmp byte [rsp+0x3bb8c {arg_3bb8c}], 'i'
1408602a9 7402 je 0x1408602ad
1408602ab eb63 jmp 0x140860310
1408602ad 48c78424308d0500… mov qword [rsp+0x58d30 {state}], 0x1
1408602b9 488b8424b88a0500 mov rax, qword [rsp+0x58ab8 {pos}]
1408602c1 48ffc0 inc rax
1408602c4 48898424b88a0500 mov qword [rsp+0x58ab8 {pos}], rax
1408602cc eb71 jmp 0x14086033f
1408602ce 48c78424308d0500… mov qword [rsp+0x58d30 {state}], 0x2
1408602da 488b8424b88a0500 mov rax, qword [rsp+0x58ab8 {pos}]
1408602e2 48ffc0 inc rax
1408602e5 48898424b88a0500 mov qword [rsp+0x58ab8 {pos}], rax
1408602ed eb50 jmp 0x14086033f
1408602ef 48c78424308d0500… mov qword [rsp+0x58d30 {state}], 0x3
1408602fb 488b8424b88a0500 mov rax, qword [rsp+0x58ab8 {pos}]
140860303 48ffc0 inc rax
140860306 48898424b88a0500 mov qword [rsp+0x58ab8 {pos}], rax
14086030e eb2f jmp 0x14086033f
The state value check is always a cmp instruction between a memory value and a immediate value, following that pattern, we can easily the dump the accepted state value and its transition. The problem remains is to filter out the failure state, actually, it was quite easy if we noticed that the only the fail state contains a standalone call instruction. So, I dumped the constraints using this script and stored that in the forms of graph in order to perform dfs to find the correct path. Here’s my solution script that contains the dump and dfs part:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import lief
import capstone
from dump import *
from tqdm import *
cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
cs.detail = True
pe: lief.PE.Binary = lief.PE.parse(r"./ntfsm.exe")
graph = {}
end_states = []
blacklist = []
for idx, addr in (enumerate(tqdm(jump_table))):
code = pe.get_content_from_virtual_address(header + addr, 10000)
cnt = 0
vertex, edge = -1, -1
edges = []
for ins in cs.disasm(code, header + addr):
if ins.mnemonic == 'call':
blacklist.append(addr)
break
if ins.mnemonic == 'cmp' and ins.operands[0].type == capstone.x86.CS_OP_MEM:
if 'byte' in ins.op_str:
vertex = ins.operands[1].imm
elif ins.mnemonic == 'je' and vertex != -1:
branch_addr = int(ins.op_str, 16)
branch = pe.get_content_from_virtual_address(branch_addr, 1000)
for br_ins in cs.disasm(branch, branch_addr):
if br_ins.mnemonic == 'inc' and br_ins.operands[0].type == capstone.x86.CS_OP_REG and br_ins.operands[0].reg == capstone.x86.X86_REG_RAX:
edges.append((vertex, edge))
vertex, edge = -1, -1
break
if br_ins.mnemonic == 'mov' and br_ins.operands[1].type == capstone.x86.CS_OP_IMM:
edge = br_ins.operands[1].imm
cnt += 1
elif ins.mnemonic == 'nop' or (ins.mnemonic == 'jmp'):
if edges != []:
graph.update({idx:edges})
break
def dfs_find_passwords(graph, start_state=0, target_length=16, max_passwords=100):
valid_passwords = []
def dfs(current_state, password, visited_states):
if len(password) == target_length:
valid_passwords.append(''.join(chr(c) for c in password))
return
if len(valid_passwords) >= max_passwords:
return
if current_state not in graph:
return
for char_code, next_state in graph[current_state]:
if visited_states.count(next_state) < 3:
new_visited = visited_states + [next_state]
dfs(next_state, password + [char_code], new_visited)
dfs(start_state, [], [start_state])
return valid_passwords
print("Searching for passwords using DFS...")
passwords = dfs_find_passwords(graph, start_state=0, target_length=16, max_passwords=50)
print(f"\nFound {len(passwords)} possible passwords:")
for i, password in enumerate(passwords):
print(f"{i+1:2d}: {password}")
Run this and we found the password: iqg0nSeCHnOMPm2Q, run the binary and we got the flag
Flag: f1n1t3_st4t3_m4ch1n3s_4r3_fun@flare-on.com
8 - FlareAuthenticator
Analyzing the binary, we can see this patterns appears a lot when the author has obfuscated function calls by computing the target function address and then store that into a rax to perform function calling like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
mov rax, cs:off_1400B2C20
mov rcx, 9E35A515A27017ABh
add rax, rcx
lea rcx, [rbp+540h+var_340]
call rax
mov rcx, [rax]
mov rax, cs:off_1400BE0E8
mov rdx, 0FB46BFF55D1567A9h
add rax, rdx
call rax
mov rcx, [rax]
mov rax, cs:off_1400A40B8
mov rdx, 0B7B2E476F5DC28B9h
add rax, rdx
call rax
mov rcx, [rbp+540h+var_3C0]
mov rax, [rax]
mov qword ptr [rax+28h], 13D5h
mov rax, cs:off_1400A4F60
mov rdx, 7F9E14D77541BCEBh
add rax, rdx
call rax
Looking more closely, we can see each block of function calls has the 2 parts like this:
1
2
<Compute call address>
<Preparing the functions argument>
Here, the idea for deobfuscate is that we move the functions argument part above and the recompute the offset of the function address to call in directly instead, and then nop all the instructions that perform calculations of the address. However, one problem still remains is that the program still calls too many functions, is there any way to resolves those calls either? Reading some of the function it calls, most of it is just small snippet like this:
1
2
3
mov rax, rcx
add rax, 20h ; ' '
retn
What if there’s enough space, we can get rid of the call instruction and patched these instructions inline with its calling function? That’s my idea and I start to implement deobfuscate script. Firstly I dumped all the start and end address of each function using this IDAPython script:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import idaapi
import idautils
import idc
OUTPUT_FILE = "functions_dump.txt" # optional output file
def dump_large_functions(min_size=0x20):
result = []
for func_ea in idautils.Functions():
func = idaapi.get_func(func_ea)
if not func:
continue
start = func.start_ea
end = func.end_ea
size = end - start
if size > min_size:
name = idc.get_func_name(start)
result.append((name, start, end, size))
# print to IDA console
print("Functions larger than 0x{:X} bytes:".format(min_size))
for name, start, end, size in result:
print(f"{name:40s} | start: 0x{start:X} | end: 0x{end:X} | size: 0x{size:X}")
# write to file
with open(OUTPUT_FILE, "w") as f:
for name, start, end, size in result:
f.write(f"{name} | start: 0x{start:X} | end: 0x{end:X} | size: 0x{size:X}\n")
print(f"\n[+] Dumped {len(result)} functions to {OUTPUT_FILE}")
# Run it
dump_large_functions(0x20)
Using those address, I wrote this script to deobfuscate all functions in the binary with this strategy, if the called functions size is enough to fit it the small block, we bring it instructions out to the calling function, else we make a function calls like normal:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
import lief
import capstone
import keystone
import struct
import sys
from parse_func import parse_functions_dump
from tqdm import tqdm
# --- Configuration ---
FILE_PATH = "./FlareAuthenticator.exe"
PATCHED_FILE_PATH = "./FlareAuthenticator_deobs_all.exe"
MASK64 = 0xFFFFFFFFFFFFFFFF
try:
pe = lief.PE.parse(FILE_PATH)
if not pe:
raise FileNotFoundError(f"Could not parse {FILE_PATH}")
except lief.bad_file as e:
print(f"Error parsing PE file: {e}")
exit()
cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
cs.detail = True
ks = keystone.Ks(keystone.KS_ARCH_X86, keystone.KS_MODE_64)
def deobfuscate_calls(FUNCTION_START_VA, FUNCTION_SIZE):
print(f"[*] Reading {FUNCTION_SIZE} bytes from VA {hex(FUNCTION_START_VA)}...")
code_bytes = bytes(pe.get_content_from_virtual_address(FUNCTION_START_VA, FUNCTION_SIZE))
instructions = list(cs.disasm(code_bytes, FUNCTION_START_VA))
patch_count = 0
patched_addresses = set()
for i, ins1 in enumerate(instructions):
if ins1.mnemonic == 'jmp' and ins1.operands[0].reg == capstone.x86.X86_REG_RAX:
patch_count += 1
pe.patch_address(ins1.address, list(b'\x90' * ins1.size))
continue
if ins1.address in patched_addresses:
continue
is_pattern_start = (
ins1.mnemonic == 'mov' and ('rip' in ins1.op_str)
)
if not is_pattern_start:
continue
print(ins1.op_str)
mov_imm_ins = None
add_ins = None
call_ins = None
intermediate_reg = None
for j in range(i + 1, min(i + 10, len(instructions))):
current_ins = instructions[j]
is_mov_imm_to_reg = (
mov_imm_ins is None and
current_ins.mnemonic in ('movabs')
)
if is_mov_imm_to_reg:
mov_imm_ins = current_ins
intermediate_reg = current_ins.operands[0].reg
continue
is_add_with_link = (
add_ins is None and intermediate_reg is not None and
current_ins.mnemonic == 'add' and
current_ins.operands[0].reg == capstone.x86.X86_REG_RAX and
current_ins.operands[1].reg == intermediate_reg
)
if is_add_with_link:
add_ins = current_ins
continue
is_call_rax = (
call_ins is None and
current_ins.mnemonic == 'call' and
current_ins.operands[0].reg == capstone.x86.X86_REG_RAX
)
if is_call_rax:
call_ins = current_ins
break
if not all([mov_imm_ins, add_ins, call_ins]):
continue
print(f"[*] Found full pattern starting at {hex(ins1.address)}")
print(f" - MOV [RIP]: {ins1.mnemonic} {ins1.op_str}")
print(f" - MOV IMM: {mov_imm_ins.mnemonic} {mov_imm_ins.op_str}")
print(f" - ADD: {add_ins.mnemonic} {add_ins.op_str}")
print(f" - CALL: {call_ins.mnemonic} {call_ins.op_str}")
try:
rip = ins1.address + ins1.size
displacement = ins1.operands[1].mem.disp
pointer_addr = rip + displacement
base_addr = int.from_bytes(pe.get_content_from_virtual_address(pointer_addr, 8), 'little')
offset = (mov_imm_ins.operands[1].imm) & MASK64
target_addr = (base_addr + offset) & MASK64
pe.patch_address(ins1.address, list(b'\x90' * ins1.size))
pe.patch_address(mov_imm_ins.address, list(b'\x90' * mov_imm_ins.size))
pe.patch_address(add_ins.address, list(b'\x90' * add_ins.size))
pe.patch_address(call_ins.address, list(b'\x90' * call_ins.size))
arg_addr = add_ins.address + add_ins.size
call_addr = call_ins.address
arg_size = call_addr - arg_addr
if arg_addr < call_ins.address:
pe.patch_address(ins1.address, list(pe.get_content_from_virtual_address(arg_addr, arg_size)))
remain = (call_addr + call_ins.size) - ins1.address - arg_size
func = bytes(pe.get_content_from_virtual_address(target_addr, 0x300))
pe.patch_address(arg_addr, list(b'\x90' * arg_size))
func_code = func.split(b'\xC3')[0]
if len(func_code) <= remain:
pe.patch_address(ins1.address + arg_size, list(func_code))
else:
cur_addr = ins1.address + arg_size
offset = target_addr - cur_addr - 5
print(hex(offset))
patch_bytes = [0xe8] + list(struct.pack("<I", offset))
print(patch_bytes)
pe.patch_address(ins1.address + arg_size, list(patch_bytes))
print(f"Patched at {hex(ins1.address + arg_size)} -> call {hex(target_addr)}\n")
patch_count += 1
for p_ins in [ins1, mov_imm_ins, add_ins, call_ins]:
patched_addresses.add(p_ins.address)
except Exception as e:
print(f"Error processing pattern at {hex(ins1.address)}: {e}")
print(f"\nDeobfuscation complete. Patched {patch_count} call sequences.")
if patch_count > 0:
print(f"Saving patched file to '{PATCHED_FILE_PATH}'...")
pe.write(PATCHED_FILE_PATH)
print("Done!")
else:
print("No matching patterns were found to patch.")
if __name__ == "__main__":
functions = parse_functions_dump('functions_dump.txt')
for start, end in tqdm(functions):
deobfuscate_calls(start, end - start)
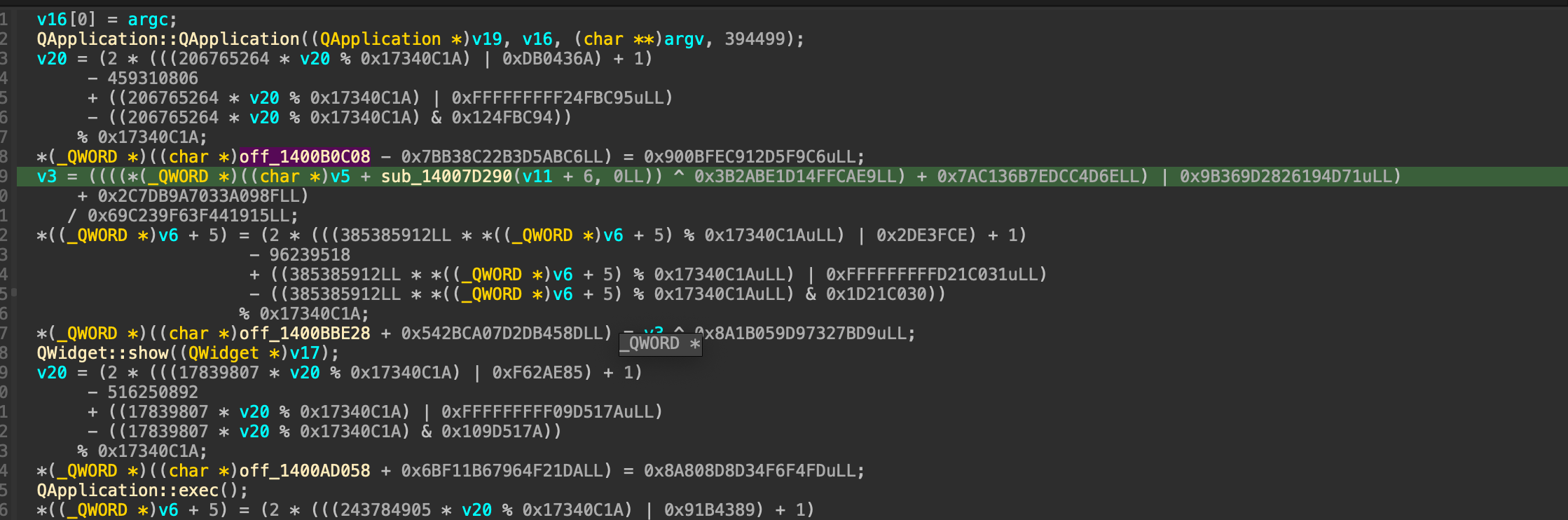
Here is the main function after initial obfuscation, we can see that it’s calling the Qt API to start Qt Application:
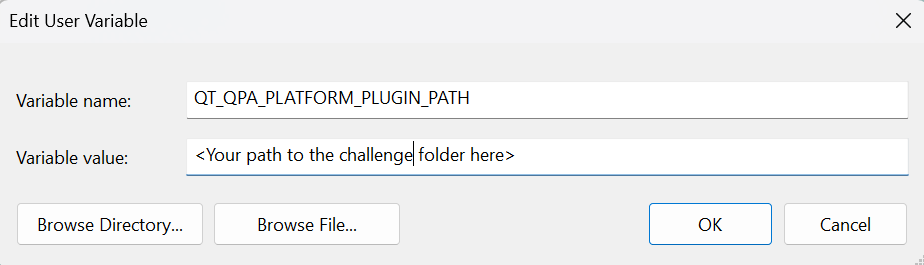
As you can see, it is still heavily MBA-obfuscated, now it’s the time for dynamic analysis. The challenge provides challengers with a run.bat file, so to run the application directly without run.bat we just need to add folder path in the Window’s Environment variable (Advanced System Settings -> Environment variables)
Then we can just clicked and run the application with no problems.
Using my experience, Qt6Core.dll (if not customed) usually handles the user input, so I used API Monitor to monitor the QtCore.dll API calls. You can do this by adding the Qt6Core.dll to the External DLL of API Monitor, and turn off Monitor DLL’s options. For each input, you can see the pattern of the Qt6 API calls, like the image below:
Using the Call Stack address I found the function where the each input is processed
The interesting thing here is that sub_140081760() is still being obfuscated because it changes the patterns from add to sub, I modify my script a little and the deobfuscation workd like normal. Also I note that is function kinda implemented an anti-decompile mechanism by adding some bytes that stop the decompiling process before the function actually ends.
1
2
3
4
5
6
7
8
nop
icebp
push rdx
mov ds:58B48000014B6E9h, al
movsb
db 0Fh
db 4
db 0
So I wrote a script to nop those bytes, and then deobs the rest of the current function. Then, I used a IDA Pro plugin d810 (https://gitlab.com/eshard/d810) to partially deobfuscate the MBA.
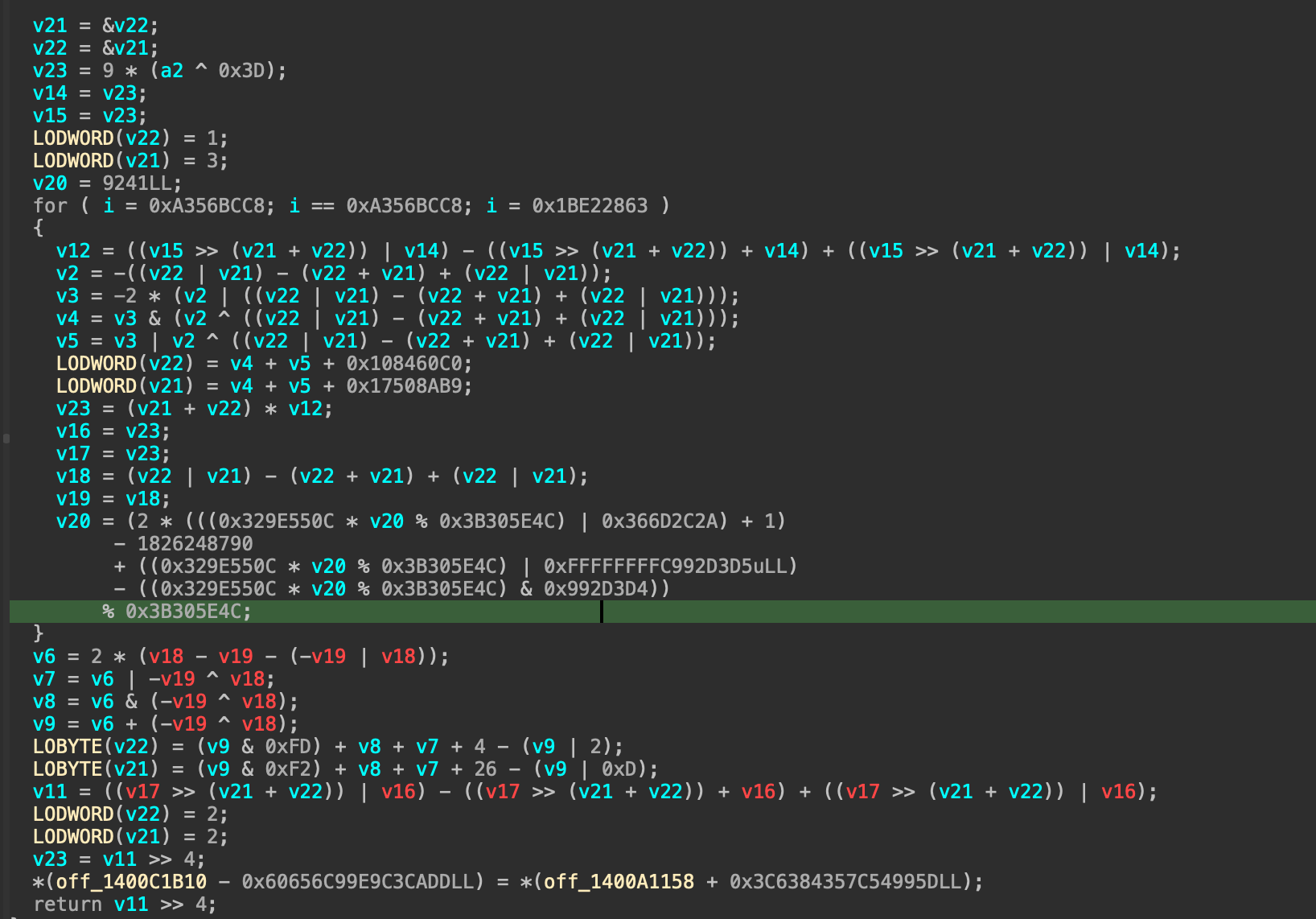
Then, after a while of “pen and paper” work(it is do-able, because when you substitute in the number, terms start to cancel out, try it and you’ll see), I finally deobfuscate that function into:
1
2
3
4
5
6
7
def gen_num(num):
a = 9 * (num ^ 0x3d)
v14 = v15 = a
v12 = (v15 >> 4) ^ v14
v23 = ((0x108460C0 + 0x17508AB9) * v12) & 0xffffffff
v11 = (v23 >> 15) ^ v23
return v11 >> 4
Then back to the calling function, it takes the ouput of the gen_num() function and then multiply with a precompute value (generated by putting calling gen_num(cur_idx) ) and the put it in total sum:
1
2
3
4
5
6
v114 = gen_num(v201, v129);
...
v35 = gen_num(v201, v113 + v122);
v99 = v35 * v114;
...
*(v201 + 15) = v99 + *(v201 + 15) - (v99 & *(v201 + 15)) + v99 + *(v201 + 15) - (v99 | *(v201 + 15));
Piece everything together, we have the calculation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
arr = [0x100, 0x200, 0x300, 0x400, 0x500, 0x600, 0x700, 0x800, 0x900, 0xa00, 0xb00, 0xc00, 0xd00, 0xe00, 0xf00, 0x1000, 0x1100, 0x1200, 0x1300, 0x1400, 0x1500, 0x1600, 0x1700, 0x1800, 0x1900]
def gen_num(num):
a = 9 * (num ^ 0x3d)
v14 = v15 = a
v12 = (v15 >> 4) ^ v14
v23 = ((0x108460C0 + 0x17508AB9) * v12) & 0xffffffff
v11 = (v23 >> 15) ^ v23
return v11 >> 4
for idx, ch in enumerate(inp):
add = arr[idx]
mult1 = gen_num(idx + 1)
mult2 = gen_num(add + ch)
total = (total + ((mult1 * mult2) & 0xffffffffffffffff)) & 0xffffffffffffffff
Back to using the API Monitor, I observed when I pressed the “OK” button to check if my input is valid, it calls QString::QString, my guess is that the API call is used for creating the strings to show on the UI, so we can trace back the validation logic from that.
Like I’ve guessed, in that function there’s 2 places that QString::QString is called, on for the correct password, the other is for incorrect password. Traceback further to the beginning, I saw a place where it checks the total sum with a hardcoded number:
Knowing our target, the problem now is how to achieve that sum. I tried with simple z3 approach but the calculating function is too non-linear which makes it hard for the SAT-solver. So I precomputed everything to make the function more linear and put it to z3 again to solve the problem:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
from z3 import *
arr = [
0x100, 0x200, 0x300, 0x400, 0x500, 0x600, 0x700, 0x800, 0x900,
0xa00, 0xb00, 0xc00, 0xd00, 0xe00, 0xf00, 0x1000, 0x1100, 0x1200,
0x1300, 0x1400, 0x1500, 0x1600, 0x1700, 0x1800, 0x1900
]
target = 0xBC42D5779FEC401
def gen_num_const(num: int) -> int:
a = (9 * (num ^ 0x3d)) & 0xffffffff
v12 = ((a >> 4) ^ a) & 0xffffffff
v23 = ((0x108460C0 + 0x17508AB9) * v12) & 0xffffffff
v11 = ((v23 >> 15) ^ v23) & 0xffffffff
return (v11 >> 4) & 0xffffffff
mult1_table = [gen_num_const(i + 1) for i in range(25)]
mult2_table = []
for add in arr:
entry = {}
for ch in range(ord('0'), ord('9') + 1):
entry[ch] = gen_num_const(add + ch)
mult2_table.append(entry)
s = Solver()
inp = [BitVec(f'inp[{i}]', 8) for i in range(25)]
for ch in inp:
s.add(ch >= ord('0'), ch <= ord('9'))
total = BitVecVal(0, 64)
for idx in range(25):
mult1 = mult1_table[idx]
term_cases = []
for ch in range(ord('0'), ord('9') + 1):
mult2 = mult2_table[idx][ch]
term_val = (mult1 * mult2) & 0xffffffffffffffff
term_cases.append((inp[idx] == ch, BitVecVal(term_val, 64)))
term = simplify(If(inp[idx] == ord('0'), BitVecVal(mult1 * mult2_table[idx][ord('0')], 64),
If(inp[idx] == ord('1'), BitVecVal(mult1 * mult2_table[idx][ord('1')], 64),
If(inp[idx] == ord('2'), BitVecVal(mult1 * mult2_table[idx][ord('2')], 64),
If(inp[idx] == ord('3'), BitVecVal(mult1 * mult2_table[idx][ord('3')], 64),
If(inp[idx] == ord('4'), BitVecVal(mult1 * mult2_table[idx][ord('4')], 64),
If(inp[idx] == ord('5'), BitVecVal(mult1 * mult2_table[idx][ord('5')], 64),
If(inp[idx] == ord('6'), BitVecVal(mult1 * mult2_table[idx][ord('6')], 64),
If(inp[idx] == ord('7'), BitVecVal(mult1 * mult2_table[idx][ord('7')], 64),
If(inp[idx] == ord('8'), BitVecVal(mult1 * mult2_table[idx][ord('8')], 64),
BitVecVal(mult1 * mult2_table[idx][ord('9')], 64)
))))))))))
total = (total + term) & BitVecVal(0xffffffffffffffff, 64)
s.add(total == target)
if s.check() == sat:
m = s.model()
result = ''.join(chr(m[inp[i]].as_long()) for i in range(25))
print("Found input:", result)
else:
print("No solution found (UNSAT)")
I found the password, which is: 4498291314891210521449296, use that in the application and then get the flag.
9 - 10000
I was kinda shocked when I see that this binary size is over 1GB, but to my surprise IDA loaded it very quickly, so there must be something going on here.
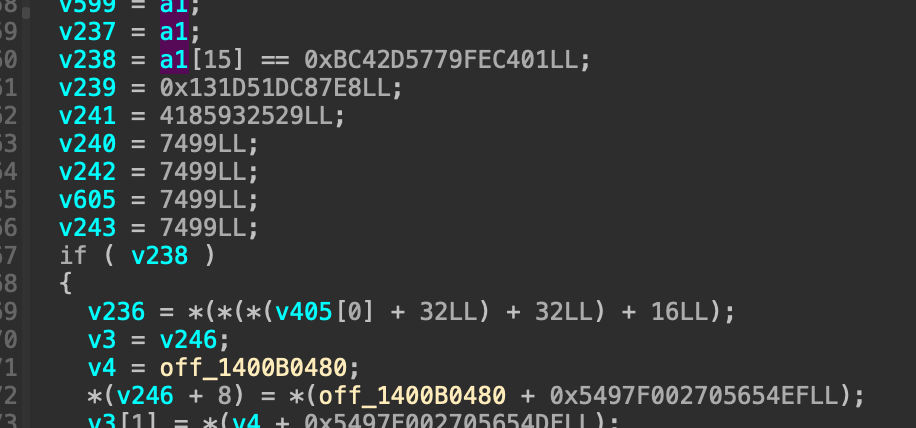
Firstly, the program requires the user to provide a 340000-byte license which split into 10000 parts. For each part, the first two bytes is processed first.
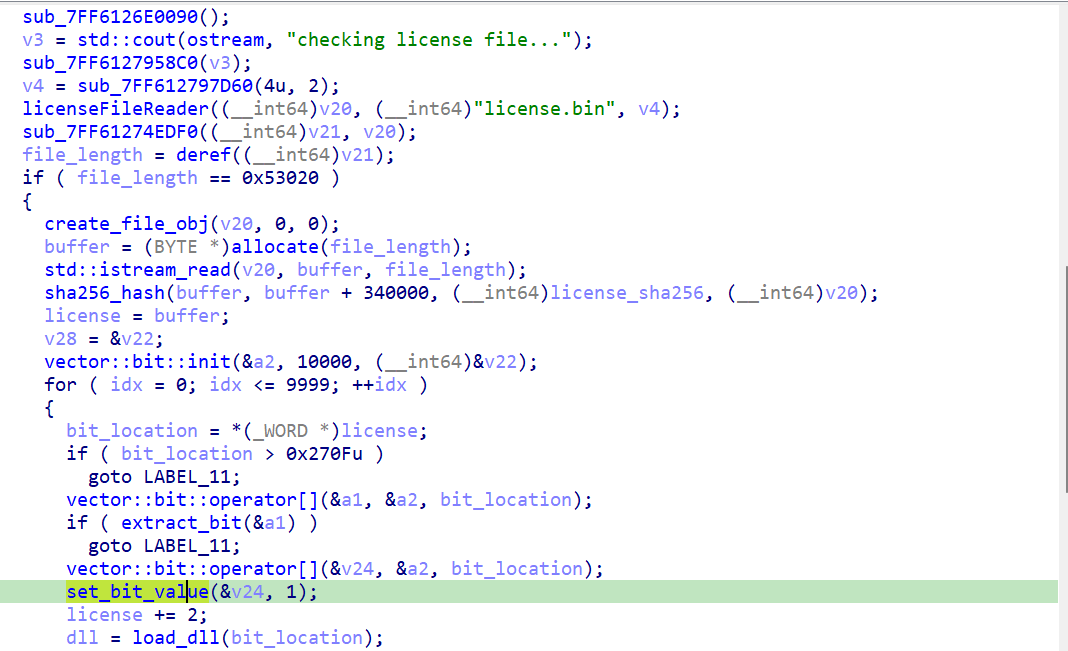
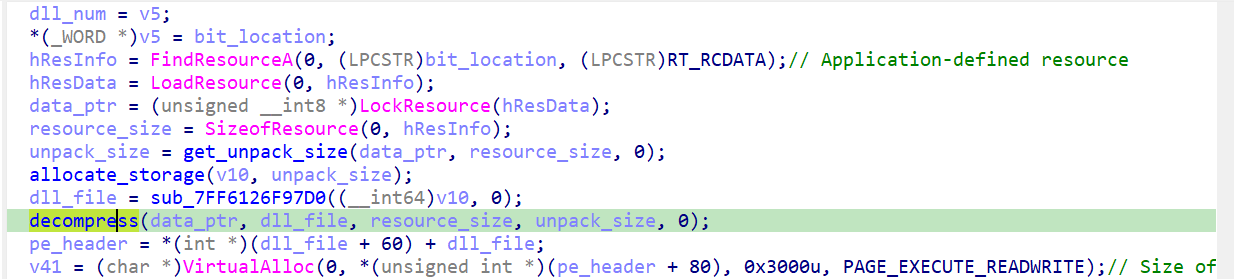
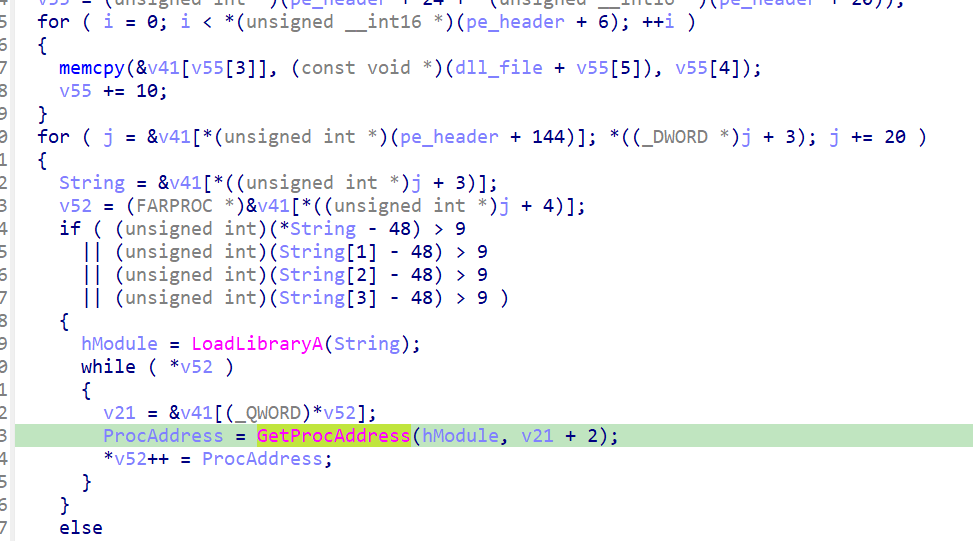
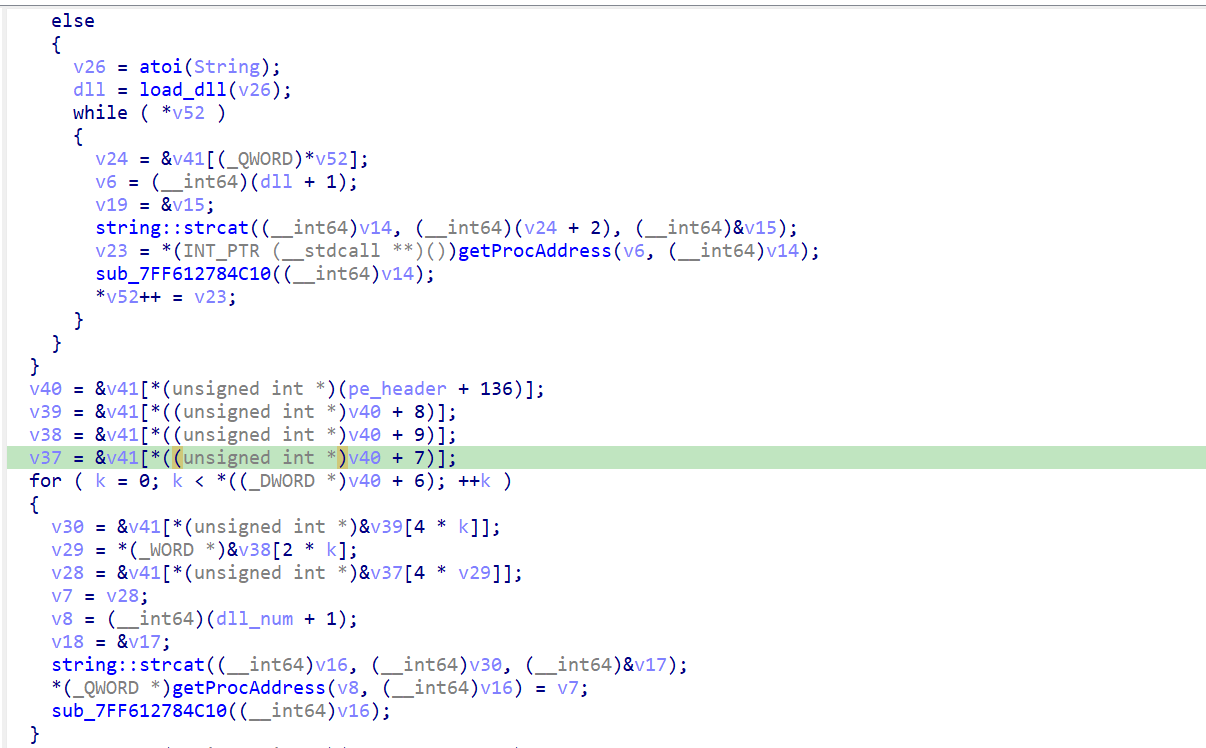
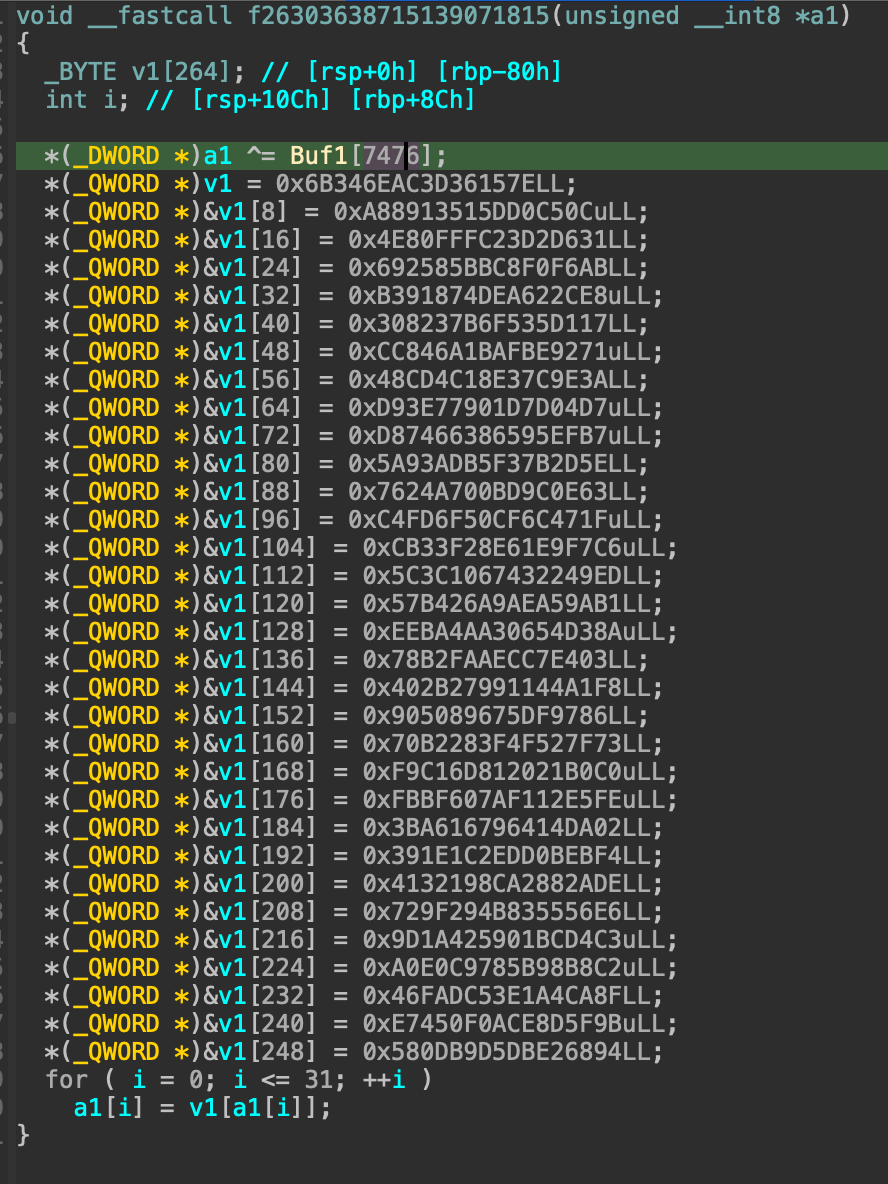
Here you can see that it loads data from the Resource sections and then decompress it, debug and dump that data, we can easily see that it’s a DLL file. Then the programs looks for the import DLLs in the IAT section of the current DLL file if it’s not loaded then the binary loads it into the running process. All the number of the DLLs in the process of each license part is stored in a vector.
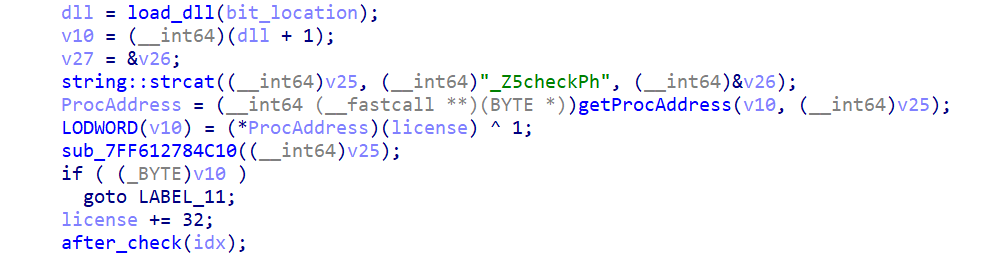
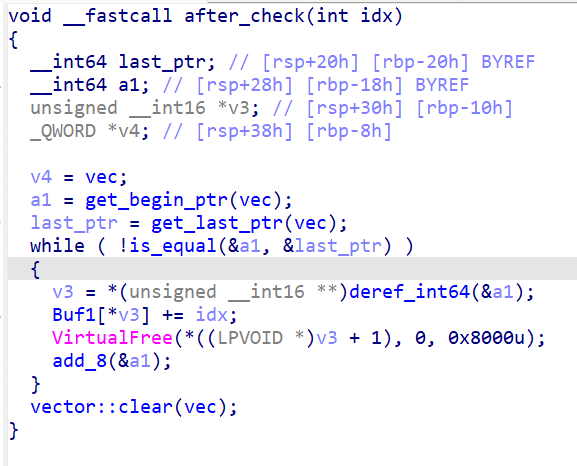
After all required DLLs has been loaded, it takes the next 32 bytes of the license, and call _Z5checkPh method of the current DLL to perform validation on the current 32-byte license part. If the part is valid, the code updated the Buf1 by adding the iteration to the index of the loaded DLLs in the current license part
If all 10000 parts of the license is correct, the program proceeds to check the order by comparing the Buf1 with a target_order
From the information above, we can split the challenge into two subproblems: “Solving the order of the DLLs” and “Solving each DLL”. But firstly, we need to dump all the DLLs stored and compressed in the Resource section of the original binary first. Here, you can easily do it by using 7z extract, but then when decompress all of them, it would take much longer because more I/O operation is executed. For a more optimal approach, I used lief to parse the binary, extract the data and reimplement the decompress to dump all the DLLs out.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import lief
import sys
from decompress_custom import *
from tqdm import *
import sys
try:
pe: lief.PE.Binary = lief.PE.parse(r"./10000.exe")
except lief.lief_errors.ParserError as e:
print(f"Error parsing file: {e}")
sys.exit(1)
if not pe or not pe.has_resources:
print("File has no resources.")
sys.exit(0)
TARGET_TYPE_ID = lief.PE.ResourcesManager.TYPE.RCDATA
for TARGET_NAME_ID in tqdm(range(0, 10000)):
found = False
for type_node in pe.resources.childs:
if type_node.id == TARGET_TYPE_ID:
for id_node in type_node.childs:
if id_node.id == TARGET_NAME_ID:
for lang_node in id_node.childs:
if not lang_node.is_data:
continue
content = lang_node.content
dll = decompress(bytes(content))
open(f'./dll_dump/{TARGET_NAME_ID}.dll', 'wb').write(dll)
I decided to solve the order of the DLLs first, the problem is simply just:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import json
lines = open('call_order_solution.txt').readlines()
call_order = []
for line in lines:
call_order.append(int(line.strip()))
with open('total_import.json', 'r') as f:
dll_import_list = json.load(f)
res = [0] * 10000
for idx, num in enumerate(call_order):
for val in dll_import_list[str(num)]:
res[val] = (res[val] + idx) & 0xffffffff
target = list(open('target_order', 'rb').read())
target = [int.from_bytes(target[i:i+4], 'little') for i in range(0, len(target), 4)]
assert(res == target)
Despite the simpliciy of the problem statement, solving it is not easy. I dumped and store all imported DLL for each DLL using this script, I used BFS instead of the a recursive approach to save time:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import lief
from tqdm import tqdm
import json
import sys
from collections import deque
dll_import = {}
target = []
call_order = []
for i in tqdm(range(0, 10000)):
binary = lief.parse(f'./dll_dump/{i}.dll')
dll_list = [i]
for lib in binary.imports:
name = lib.name.split('.dll')[0]
try:
dll_list.append(int(name))
except:
continue
dll_import.update({i:dll_list})
total_import = {}
for key in tqdm(dll_import.keys()):
visited = set()
result = []
queue = deque([key])
while queue:
current = queue.popleft()
if current not in visited:
visited.add(current)
result.append(current)
queue.extend(dll_import[current])
total_import[key] = result
with open('total_import.json', 'w') as f:
json.dump(total_import, f)
Now, we can rewrite the problem in a more mathematical way. We’re looking for the call_order array, which is a permutation of [0, 1, ..., 9999]. Let’s define an inverse array X where X[k] is the index (or position) of DLL k in the call_order. The call order logic now can be stated as follow:
For every DLL \(v\) from \(0\) to \(9999\):
\[T[v] = \left(\sum_{k \text{ where } v \text{ is a dependency of } k} X[k]\right) \bmod 2^{32}\]This is a massive system of 10,000 linear equations with 10,000 unknowns (the X array). We can write this in matrix form as:
\[T = A \times X\]Where:
\(T\) is the
target_ordervector.\(X\) is the vector of unknown indices we want to find.
\(A\) is a \(10000 \times 10000\) matrix where \(A[v, k] = 1\) if \(v\) is in
total_import_list[k](meaning DLL \(v\) is a transitive dependency of DLL \(k\)), and \(0\) otherwise.
Solving a \(10000 \times 10000\) system modulo \(2^{32}\) is computationally infeasible. In order to address that issue, I started analyzing more on characteristics of them problem. We know that our solution X is a permutation of [0, ..., 9999]. This means all values in \(X\) are less than \(10000\). This suggests that instead of solving the system modulo \(2^{32}\), we can try to solve it modulo \(N = 10000\)
This is much more manageable, but inverting a \(10000 \times 10000\) matrix is still too slow. I also noted that the DLL dependencies form a Directed Acyclic Graph (DAG). If we build a graph of DLL and then we sorted it topologically. This it gives us an ordering of DLLs from least dependent (has no dependencies) to most dependent. Because \(A[v, k] = 1\) only if \(v\) is a dependency of \(k\) (Note that a DLL \(k\) can only depend on DLLs that come before it in the topological sort). Then, we have an upper triangular matrix, solving it with backward substitution and we have the call order of the DLLs solved.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import json
import sys
from tqdm import tqdm
from collections import deque
N = 10000
SOLVE_MOD = N
VERIFY_MOD = 0xffffffff + 1
target_bytes = open('target_order', 'rb').read()
T_full = [int.from_bytes(target_bytes[i:i+4], 'little')
for i in range(0, N * 4, 4)]
T_mod_N = [val % SOLVE_MOD for val in T_full]
with open('dll_import.json', 'r') as f:
dll_import_str = json.load(f)
G_0 = {int(k): [] for k in dll_import_str}
G_0_inv = {int(k): [] for k in dll_import_str}
for k_str, dependencies in dll_import_str.items():
k_int = int(k_str)
for v in dependencies:
if v != k_int:
G_0[k_int].append(v)
G_0_inv[v].append(k_int)
with open('total_import.json', 'r') as f:
D_str_keys = json.load(f)
D = {int(k): set(v) for k, v in D_str_keys.items()}
in_degree = {k: 0 for k in range(N)}
for k in range(N):
for v in G_0[k]:
in_degree[k] += 1
queue = deque([k for k in range(N) if in_degree[k] == 0])
topo_order = []
while queue:
k = queue.popleft()
topo_order.append(k)
for v in G_0_inv[k]:
in_degree[v] -= 1
if in_degree[v] == 0:
queue.append(v)
X = [0] * N
topo_order_index_map = {dll_id: index for index, dll_id in enumerate(topo_order)}
for v in tqdm(reversed(topo_order), desc="Solving for X"):
current_sum = 0
v_topo_index = topo_order_index_map[v]
for k_topo_index in range(v_topo_index + 1, N):
k = topo_order[k_topo_index]
if v in D[k]:
current_sum = (current_sum + X[k]) % SOLVE_MOD
X[v] = (T_mod_N[v] - current_sum + SOLVE_MOD) % SOLVE_MOD
P = [0] * N
for k in range(N):
idx = X[k]
P[idx] = k
R_mod_32 = [0] * N
for i in tqdm(range(N), desc="Verifying"):
k = P[i]
for v in D[k]:
R_mod_32[v] = (R_mod_32[v] + i) % VERIFY_MOD
assert R_mod_32 == T_full
with open('call_order_solution.txt', 'w') as f:
for num in P:
f.write(f"{num}\n")
print("Solution saved to 'call_order_solution.txt'.")
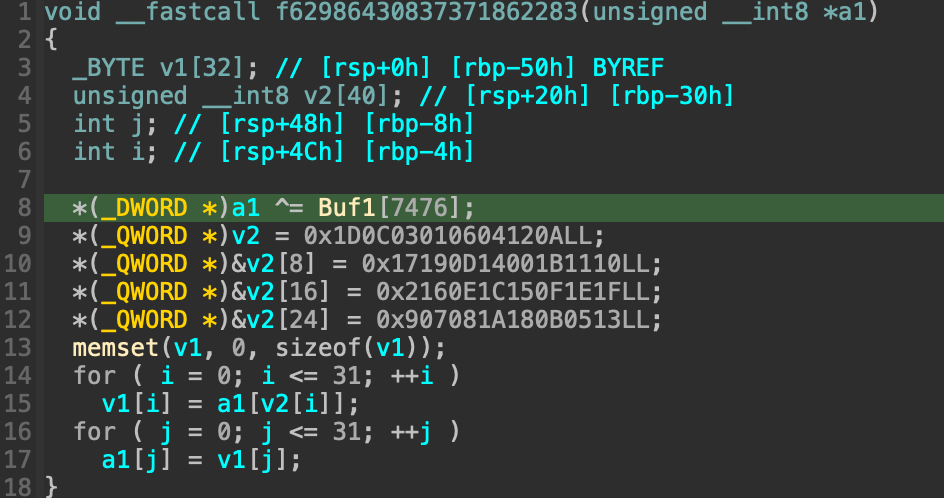
Now half of our problem is solved, next objective is to solve the license for each DLL. From the order results, I open the first DLL in the order which is 7476 (you can see some problems with the calling convention of the decompiled code in IDA, using Options \(\rightarrow\) Compiler \(\rightarrow\) Change Compiler to Visual C++ and everything should work fine) we can see that calls a lot of transformation function on our 32-byte input sub-license.
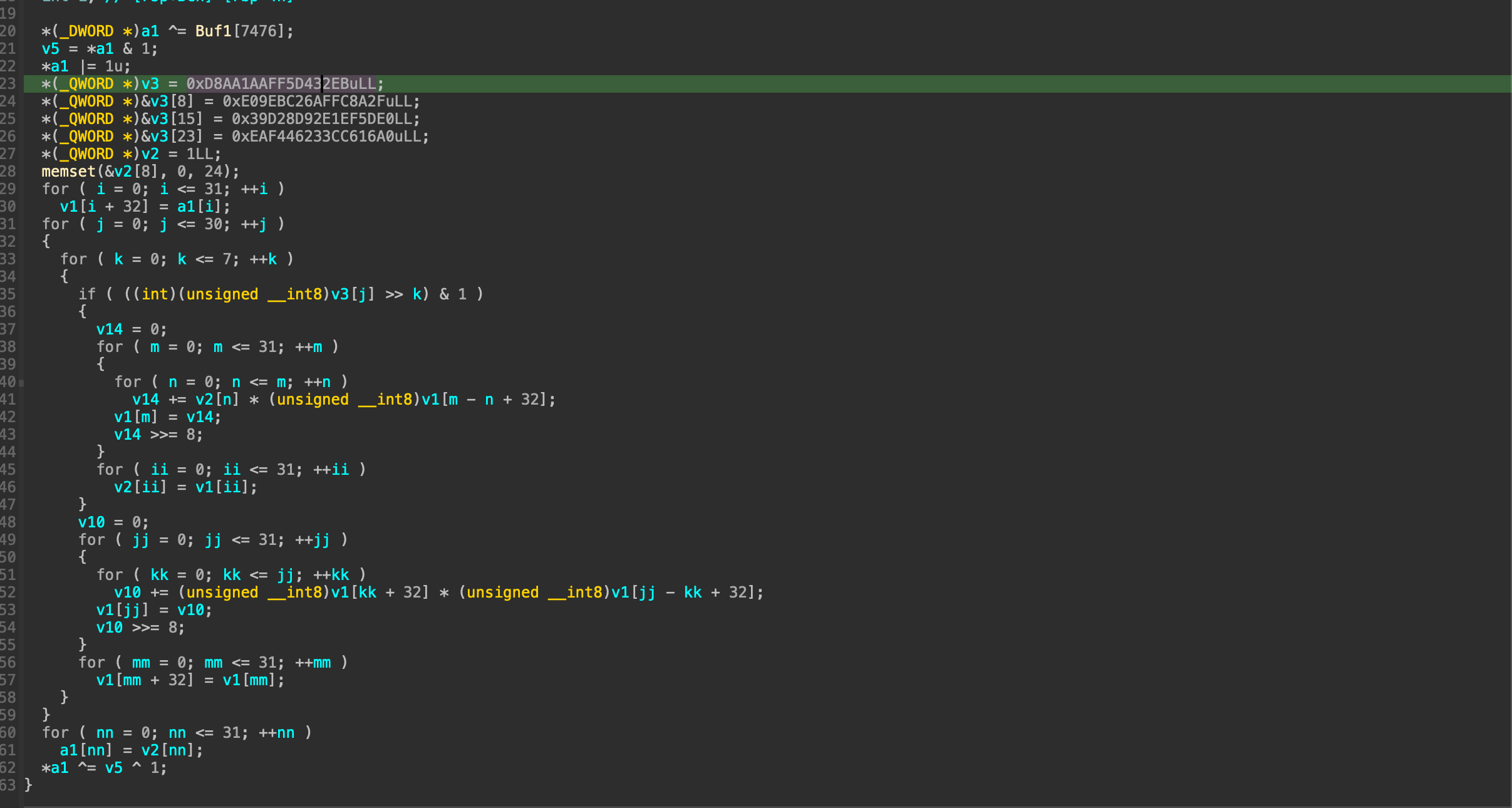
And all the transform functions, it has a large block of code. Analyzing that block clearly, I have reconstructed the transformation like this. Firstly it loads the constants and then xored with the transformed license. Then it split it into a \(4 \times 4\) matrix to perform modular exponentiation with hardcoded exponent, and modulus. Then, it takes that matrix to compare with another embedded matrix in the code (these constants are different for each DLL).
In Mathematical notation, it should be like this:
\[(M_{init} \oplus L_{transformed}) ^ e \pmod{P} \equiv M_{target}\]Where:
- \(M_{init}\) is the bytes hardcoded to xor with the transformed license
- \(L_{transformed}\) is the licensed after being transformed by function calls above.
- \(M_{target}\) is the target matrix
Further simpilify it, we set \(M_{base} = M_{init} \oplus L_{transformed}\), because the xor operation is not to hard to reverse. Then our job now is to find \(M_{base}\) such that \(M_{base} ^ e \pmod{p} \equiv M_{target}\)
I asked LLM to help me on how to solve this equation, and it gave me this script:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sage.all import *
def solve(P_MOD, EXPONENT, M_BASE_INIT, GOLDEN_MATRIX):
K = Zmod(P_MOD)
G_matrix_base = Matrix(K, 4, 4, M_BASE_INIT)
G_golden_base = Matrix(K, 4, 4, GOLDEN_MATRIX)
v = G_golden_base.multiplicative_order()
d = power_mod(EXPONENT, -1, v)
G2 = G_golden_base ** d
M_base_solved = [int(x) for x in G2.list()]
key_parts = [0] * 4
key_parts[0] = M_BASE_INIT[0] ^ M_base_solved[0]
key_parts[1] = M_BASE_INIT[1] ^ M_base_solved[1]
key_parts[2] = M_BASE_INIT[2] ^ M_base_solved[2]
key_parts[3] = M_BASE_INIT[3] ^ M_base_solved[3]
license_bytes = struct.pack('<4Q', *key_parts)
return license_bytes.hex()
Miraculously, it worked, and now 80% of the job is done. Looking back at those functions above, after a while of careful observation, I can conclude that it only has 3 types of function, the first type of function is just simple bytes substitution with different hardcoded sbox in each one of the type.
The second type is shuffle:
I reversed it like this:
1
2
3
4
5
6
7
8
9
10
11
12
def invert_transform_2(data: bytearray, xor_key: int, pbox: list[int]):
if len(data) < 32 or len(pbox) != 32:
raise ValueError("Data and P-box must be at least 32 bytes long.")
original_data_copy = bytes(data)
for i in range(32):
data[pbox[i]] = original_data_copy[i]
original_dword = int.from_bytes(data[0:4], 'little')
xored_dword = original_dword ^ xor_key
data[0:4] = xored_dword.to_bytes(4, 'little')
return data
And for the third and last type of transformation is \(out = (((L_{in} \oplus xor\_key) \lor 1) ^ E) \pmod {2^{256}} \oplus (((L_{in} \oplus xor\_key) \pmod 2) \oplus 1)\)
This can be reversed with this function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def invert_transform_3(output: bytes, buf1_7476: int, constant):
assert len(output) == 32
mod = 1 << 256
v4 = bytearray(40)
consts = [
(constant[0], 0),
(constant[1], 8),
(constant[2], 15),
(constant[3], 23)
]
for val, off in consts:
v4[off:off+8] = val.to_bytes(8, 'little')
E = int.from_bytes(v4[:31], 'little')
def inv_mod_pow2(e, bits=255):
inv = 1
for _ in range(bits.bit_length()):
inv = (inv * (2 - e * inv)) & ((1 << bits) - 1)
return inv
E_inv = inv_mod_pow2(E, 255)
R_int = int.from_bytes(output, 'little')
results = []
for orig_lsb in (0, 1):
R2 = R_int ^ (orig_lsb ^ 1)
B = pow(R2, E_inv, mod)
if orig_lsb == 0:
B &= ~1
else:
B |= 1
B ^= buf1_7476
results.append((orig_lsb, B.to_bytes(32, 'little')))
return results
One more note here is that, as you see at the beginning of everything transformation, there’s a small xor part, that xor key is actually Buf1 in the 10000.exe binary which used to check the call_order, so when dumping constants and transformation order from those binary, make sure to keep track of which DLL that function belongs to. Now, everything is clear, the thing we have to do now is to extract the constants and the transform order from 10000 DLLs. Here is my script for doing it:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import lief
import capstone
import sys
import json
from tqdm import *
cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
cs.detail = True
mask64 = 0xffffffffffffffff
def dump_const_typ1(instructions):
constants = []
start = 12
if instructions[11].mnemonic == 'movabs':
start = 11
for i in range(start, len(instructions), 4):
constants += [instructions[i].operands[1].value.imm & mask64, instructions[i+1].operands[1].value.imm & mask64]
assert (instructions[i].operands[1].value.imm & mask64) > 1000
assert (instructions[i+1].operands[1].value.imm & mask64) > 1000
if len(constants) == 32:
break
return constants
def find_function_name(address):
for entry in pe.exported_functions:
if entry.address == address:
return entry.name
if pe.has_imports:
for imported_lib in pe.imports:
for imported_func in imported_lib.entries:
if imported_func.iat_address == address:
return f"{imported_lib.name}!{imported_func.name}"
return "unknown"
def find_import_by_iat_location(iat_rva):
if pe.has_imports:
for imported_lib in pe.imports:
for imported_func in imported_lib.entries:
if imported_func.iat_address == iat_rva:
return f"{imported_lib.name}!{imported_func.name}"
return "unknown"
def dump_const_typ2(instructions):
constants = []
start = 12
if instructions[11].mnemonic == 'movabs':
start = 11
for i in range(start, len(instructions), 4):
constants += [instructions[i].operands[1].value.imm & mask64, instructions[i+1].operands[1].value.imm & mask64]
assert (instructions[i].operands[1].value.imm & mask64) > 1000
assert (instructions[i+1].operands[1].value.imm & mask64) > 1000
if len(constants) == 4:
break
return constants
def dump_const_typ3(instructions):
constants = []
start = 22
if instructions[21].mnemonic == 'movabs':
start = 21
for i in range(start, len(instructions), 4):
constants += [instructions[i].operands[1].value.imm & mask64, instructions[i+1].operands[1].value.imm & mask64]
assert (instructions[i].operands[1].value.imm & mask64) > 1000
assert (instructions[i+1].operands[1].value.imm & mask64) > 1000
if len(constants) == 4:
break
return constants
total_constant = {}
for i in tqdm(range(0, 10000)):
pe = lief.parse(f'./dll_dump/{i}.dll')
export_functions = {}
func_calls = []
check_consts = []
for entry in pe.exported_functions:
func_name = entry.name
# print(func_name)
func_rva = entry.address
func_offset = pe.rva_to_offset(func_rva)
section = pe.section_from_rva(func_rva)
if entry.name != '_Z5checkPh':
if section:
func_bytes = section.content[func_offset - section.offset:func_offset - section.offset + 0x204]
instructions = list(cs.disasm(func_bytes, func_rva))
if instructions[12].mnemonic == 'movabs':
if instructions[20].operands[1].type == capstone.x86.X86_OP_IMM and instructions[20].operands[1].value.imm != 0:
typ = 1
constants = dump_const_typ1(instructions)
else:
typ = 2
constants = dump_const_typ2(instructions)
else:
typ = 3
constants = dump_const_typ3(instructions)
export_functions.update({entry.name:(typ, constants)})
else:
func_bytes = section.content[func_offset - section.offset:func_offset - section.offset + 0x4e7f + 2000]
instructions = list(cs.disasm(func_bytes, func_rva))
last_mov_rax = None
stop_flag = 0
for ins in instructions:
if ins.mnemonic == 'mov' and 'rax' in ins.op_str and stop_flag == 0:
if ins.operands[1].type == capstone.x86.X86_OP_MEM:
if ins.operands[1].value.mem.base == capstone.x86.X86_REG_RIP:
target_rva = ins.address + ins.size + ins.operands[1].value.mem.disp
last_mov_rax = target_rva
elif ins.mnemonic == 'call' and stop_flag == 0:
if ins.operands[0].type == capstone.x86.X86_OP_IMM:
target = ins.operands[0].value.imm
target_name = find_function_name(target)
func_calls.append(target_name)
elif ins.operands[0].type == capstone.x86.X86_OP_REG:
if last_mov_rax:
target_name = find_import_by_iat_location(last_mov_rax)
func_calls.append(target_name)
last_mov_rax = None
else:
raise('Sadge -> Something wrong')
elif ins.mnemonic == 'movabs' and ins.operands[0].type == capstone.x86.X86_OP_REG and ins.operands[0].reg == capstone.x86.X86_REG_RAX:
stop_flag = 1
# print(hex(ins.operands[1].value.imm & mask64))
check_consts.append(ins.operands[1].value.imm & mask64)
else:
if ins.mnemonic == 'retn':
break
check_consts = check_consts[:34]
export_functions.update({'func_order': func_calls})
export_functions.update({'check_consts': check_consts})
assert(len(check_consts) == 34)
total_constant.update({f'{i}':export_functions})
with open('total_constant.json', 'w') as f:
json.dump(total_constant, f)
Note that to get the symbols of the imported functions, I utilized the Import Address Table(IAT), to find its address. Now, let’s get to the automation part, I solved 10000 4x4 modular exponentiation matrix first using:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import struct
import math
import sys
import json
from sage.all import *
def solve2(P_MOD, EXPONENT, M_BASE_INIT, GOLDEN_MATRIX):
K = Zmod(P_MOD)
G_matrix_base = Matrix(K, 4, 4, M_BASE_INIT)
G_golden_base = Matrix(K, 4, 4, GOLDEN_MATRIX)
v = G_golden_base.multiplicative_order()
d = power_mod(EXPONENT, -1, v)
G2 = G_golden_base ** d
M_base_solved = [int(x) for x in G2.list()]
key_parts = [0] * 4
key_parts[0] = M_BASE_INIT[0] ^ M_base_solved[0]
key_parts[1] = M_BASE_INIT[1] ^ M_base_solved[1]
key_parts[2] = M_BASE_INIT[2] ^ M_base_solved[2]
key_parts[3] = M_BASE_INIT[3] ^ M_base_solved[3]
license_bytes = struct.pack('<4Q', *key_parts)
return license_bytes.hex()
from tqdm import trange
if __name__ == "__main__":
import json
with open('total_constant.json') as f:
total_constant = json.loads(f.read())
license_for_dll = {}
for i in trange(0, 10000):
check_consts = total_constant[f'{i}']['check_consts']
P_MOD = check_consts[0]
EXPONENT = check_consts[1]
M_BASE_INIT = check_consts[2:18]
GOLDEN_MATRIX = check_consts[18:34]
license_bytes = solve2(P_MOD, EXPONENT, M_BASE_INIT, GOLDEN_MATRIX)
license_for_dll.update({i:license_bytes})
with open('matrix_sol.json', 'w') as f:
json.dump(license_for_dll, f)
Then, after saving everything into json files, I just loaded and run the final script to solve the license:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import json
from tqdm import *
from inv_check_3 import *
from inv_check_2 import *
import struct
from tqdm import *
with open('total_constant.json') as f:
total_constant = json.loads(f.read())
with open('total_import.json') as f:
total_import = json.loads(f.read())
with open('matrix_sol.json') as f:
matrix_sol = json.loads(f.read())
lines = open('call_order_solution.txt').readlines()
call_order = [line.strip() for line in lines]
box = [0] * 10000
sol = {}
for idx, call_dll in enumerate(call_order):
a = bytes.fromhex(matrix_sol[call_dll])
for func_name in tqdm(total_constant[call_dll]['func_order'][::-1]):
if 'dll' in func_name:
dll, func_name = func_name.split('.dll!')
dll = str(int(dll))
func = total_constant[dll][func_name]
else:
dll = call_dll
func = total_constant[call_dll][func_name]
typ, const = func
xor_key = box[int(dll)]
if typ == 3:
out = invert_transform_3(a, xor_key, const)
for bit, candidate in out:
if candidate.hex().count('0') < 40:
a = candidate
break
elif typ == 2:
shuffle = []
for val in const:
shuffle += list(struct.pack("<Q", val))
a = invert_transform_2(bytearray(a), xor_key, shuffle)
elif typ == 1:
sbox = []
for val in const:
sbox += list(struct.pack("<Q", val))
a = list(a)
for i in range(len(a)):
a[i] = sbox.index(a[i])
original_dword = int.from_bytes(a[0:4], 'little')
xored_dword = original_dword ^ xor_key
a[0:4] = xored_dword.to_bytes(4, 'little')
a = bytes(a)
for val in total_import[call_dll]:
box[val] = (box[val] + idx) & 0xffffffff
print(a.hex())
sol.update({call_dll:a.hex()})
with open('solution', 'w') as f:
json.dump(sol, f)
And then generate the craft the license and generate the flag from the AES_CBC decryption (You can find it in the 10000.exe binary when the checking is correct)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import json
lines = open('call_order_solution.txt').readlines()
call_order = [line.strip() for line in lines]
with open('solution.json') as f:
dll_solution = json.loads(f.read())
license_bin = b''
for call_dll in call_order:
dll = int(call_dll)
license_bin += dll.to_bytes(2, 'little')
license_bin += bytes.fromhex(dll_solution[call_dll])
open('license.bin', 'wb').write(license_bin)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from Crypto.Cipher import AES
import hashlib
iv = [
0x78, 0x61, 0x53, 0x38, 0xBC, 0xB1, 0xF1, 0x80, 0xD3, 0x4E,
0xD1, 0xFA, 0x47, 0xA4, 0x1D, 0x3D
]
license_bin = open('license.bin', 'rb').read()
sha256 = hashlib.sha256()
sha256.update(license_bin)
key = sha256.digest()
ct = [
0xA1, 0xA6, 0x10, 0x48, 0x3E, 0xBD, 0x82, 0x5C, 0xE1, 0xE0,
0x0D, 0x72, 0x2D, 0xF6, 0x8D, 0xCF, 0xF7, 0x0C, 0xAC, 0x1E,
0x64, 0xA4, 0xFC, 0xA7, 0x44, 0x0B, 0x5A, 0xBC, 0x61, 0x72,
0x59, 0xCE, 0x66, 0xF7, 0xE0, 0x71, 0x7B, 0x57, 0x51, 0xA3,
0xBF, 0x5F, 0x6C, 0x9D, 0xEE, 0x1C, 0x17, 0xBC, 0x88, 0x1C,
0x2C, 0x17, 0xA0, 0xD8, 0x03, 0x2F, 0x36, 0x9A, 0x00, 0xBA,
0x32, 0x09, 0xC4, 0xF5, 0x69, 0xD2, 0xCD, 0x47, 0x29, 0xB6,
0xB4, 0xBA, 0xBB, 0x6B, 0x35, 0xF0, 0xD5, 0x04, 0xF2, 0x5D,
0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00,
0x00, 0x00, 0x00, 0x00, 0x00, 0x00
]
cipher = AES.new(key, AES.MODE_CBC, bytes(iv))
plaintext = cipher.decrypt(bytes(ct))
print(plaintext.decode())
Finally, I got the flag for this challenge: Its_l1ke_10000_spooO0o0O0oOo0o0O0O0OoOoOOO00o0o0Ooons@flare-on.com
Conclusion
This is a very memorable first Flare-on season for me, I learned so much during one month of try-harding and suffering also. Thank you so much for reading my writeups.